Number System
Types of number
| Type | Value |
|---|---|
| Natural Numbers | $N=1,2,3,4, \ldots$ |
| Prime Number | $P=2,3,5,7,11,13,17, \ldots$ |
| Composite Number | $4,6,8,9,10,12, \ldots$ |
| Whole Numbers | $W=0,1,2,3,4, \ldots$ |
| Integers | $Z= \ldots,−3,−2,−1,0,1,2,3, \ldots$ |
| Rational Numbers | $Q= \frac{1}{2} ,0.33333 \ldots,52,1110, \ldots$ |
| Irrational Numbers | $F= \ldots ,π, \sqrt{2} ,0.121221222 \ldots$ |
| Real Numbers | $R= \ldots ,−3,−1,0, \frac{1}{5},1.1, \sqrt{2} ,2,3,π, \ldots$ |
| Complex Number | $C= \ldots ,−3+2i,0,1+3i, \ldots$ |
Types of number system
Number system consists values from 0 to N-1
| Number System | Value |
|---|---|
| Binary | 0 and 1 |
| Octal | 0 to 7 |
| Decimal | 0 to 9 |
| HexaDecimal | 0 to 9 and A to F |
Number Series
| Series | Formula |
|---|---|
| Sum of first n numbers | $ \frac{n \cdot (n+1)}{2} $ |
| Squares of first n numbers | $ \frac{n \cdot (n+1) \cdot (2n+1)}{6} $ |
| Cube of first n numbers | $ (\frac{n \cdot (n+1)}{2})^2 $ |
| Sum of first n even numbers | $ n \cdot (n+1) $ |
| Sum of first n odd numbers | $ n^2 $ |
Number Sequences
Arithmetic progression
$2, 4, 6, 8, \ldots$
$\rightarrow a_{1} = a + 0.d $
$\rightarrow a_{2} = a + 1.d $
$\rightarrow a_{3} = a + 2.d $
$ \vdots $
$\rightarrow T_{n} = a + (n-1) \cdot d $
We know that
$\rightarrow avg = \frac{sum}{n}$
$\rightarrow sum = avg \times n$
And in case of evenly distributed numbers
$\rightarrow avg = \frac{first + last}{2}$
$\rightarrow sum = \frac{(a + a + (n-1).d)n}{2}$
$\rightarrow S_n = \frac{n(2a + (n-1)*d)}{2}$
Geometric progression
2, 4, 16, 32, 64 ……
a, $a.r^{1}$, $a.r^{2}$, $a.r^{3}$, … $r^{n-1}$
Nth term $\rightarrow$ $T_{n} = a*r^{n-1}$
Sum till N terms $\rightarrow$ $S_{n} = a*(r^{n} - 1)/ r-1$
Sum of infinite terms $\rightarrow$ $S_{\infty} = \frac{a}{1-r}$
Harmonic Progression
Harmonic progression (or harmonic sequence) is a progression formed by taking the reciprocals of an arithmetic progression. $\rightarrow \frac{1}{5}, \frac{1}{10}, \frac{1}{15}, \ldots$
Nth term $\rightarrow$ $T_{n} = \frac{1}{a + (n-1) \cdot d}$
Average
Mean
The central of middle value in a set of data. Commons ways to calculate average are mean, median, mode.
Suppose
$a_{1}, a_{2}, a_{3}, …. , a_{n}$
Mean is the arithmetic average of a given data.
$\rightarrow mean = \frac{a_{1} + a_{2} + a_{3} + …. + a_{n}}{n}$
Types of Mean
| Number | Test |
|---|---|
| Arithmetic Mean(AM) | $\frac{a+b}{2}$ |
| Geometric Mean(GM) | $\sqrt{ab}$ |
| Harmonic Mean(HM) | $ (2ab) \cdot (a+b) $ |
$\rightarrow GM^2 = AM \times GM $
Median
Median is the middle value
$\rightarrow median = A[\frac{n+1}{2}] if n is odd else \frac{A[\frac{n}{2}] + A[\frac{n+1}{2} + 1]}{2} $
Mode
Mode is the number with the maximum frequency
$\rightarrow 3 Median = 2 Mean + Mode $
Quadratic formula
Roots of quad eq.
$ax^{2} + by + c = 0$
$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$.
$D = b^{2} - 4ac$
- D < 0 : Imaginary roots
- D = 0 : Two equal roots
- D > 0 : Two distinct roots
Prime numbers
2,3,5,7,11, ….
All the numbers having exactly two factors.
Can be represented as 6n+1 or 6n-1, except 2 and 3.
2 and 3 are only consecutive prime numbers.
Test Of Divisibility
| Number | Test |
|---|---|
| 2 | Last one digit is divisible by 2 (Unit digist is 0, 2, 4, 6, 8) |
| 3 | Sum is divisble by 3 |
| 4 | Last two digit is divisible by 4 |
| 5 | Unit digit is either 0 or 5 |
| 6 | Divisible by both 2 and 3 |
| 7 | Difference between twice the unit digit of the given number and the remaining part is divisible by 7 |
| 8 | Last three digit is divisible by 8 |
| 9 | Sum is divisble by 9 |
| 10 | Unit digit is 0 |
| 11 | Difference between sum of digits at odd places and even places is either 0 or is divisible by 11 |
HCF and LCM
There are three ways to find HCM and LCM
- Listing factors/multiple
- Prime fractorization
- Division method
$\rightarrow a\times b = HCF(a,b) \times LCM(a,b)$
HCF of co-primes is 1.
For fractions
$ HCF = \frac{HCF(Numerators)}{LCM(Denominators)} $
$ LCM = \frac{LCM(Numerators)}{HCF(Denominators)} $
Area
Rectangle
$\rightarrow area = length \times bread$
$\rightarrow perimeter = 2 ( length + bread)$
Square
$\rightarrow area = side^{2} $
$\rightarrow perimeter = 4 \times side$
Rhombus
$\rightarrow area = \frac{product of diagonals}{2} $
Equilateral Triangle
$\rightarrow area = \frac{ \sqrt{n} \times side^{2}}{4} $
$\rightarrow radius of incircle = \frac{side}{2 \times \sqrt{3}} $
$\rightarrow radius of circle = \frac{side}{\sqrt{3}} $
Isosceles Triangle
$\rightarrow area = \frac{base \times length}{2} $
Heron’s Formula
$\rightarrow area = \sqrt{s(s-a)(s-b)(s-c)} $
where s is semi-perimeter
$\rightarrow s = \frac{a + b + c}{2}$
Circle
$\rightarrow area = \pi \times R^{2} $
$\rightarrow circumference = 2 \times \pi \times R $
Parallelogram
$\rightarrow area = base \times height $
Volume
Cuboid
$\rightarrow Volume = L \ast B \ast H $
$\rightarrow Surface area = 2 \cdot (LB + BH + LH) $
$\rightarrow Diagonal = \sqrt{L^2 + B^2 + H^2} $
Cube
$\rightarrow Volume = a^3 $
$\rightarrow Surface area = 6 \cdot a^2 $
$\rightarrow Diagonal = \sqrt{3}a $
Cylinder
$\rightarrow Volume = \pi r^2h $
$\rightarrow Curved surface area = 2 \pi rh $
$\rightarrow Total surface area = 2 \pi rh + 2 \pi r^2 $
Cone
$\rightarrow Slant height = \sqrt{h^2 + r^2} $
$\rightarrow Volume = \frac{\pi r^2 h}{3} $
$\rightarrow Curved surface area = \pi rL $
$\rightarrow Total surface area = \pi rL + \pi r^2 $
Sphere
$\rightarrow Volume = \frac{4 \pi r^3}{3} $
$\rightarrow Surface area = 4 \pi r^2 $
Trignometry
$Radian = \frac{\pi}{180} \times θ$
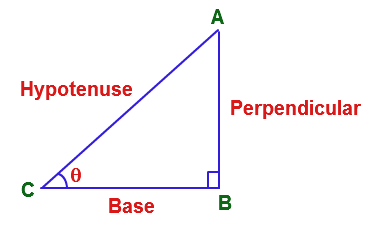
Trignometric Ratios
$ sin θ = \frac{Perpendicular}{Hypotenuse} $
$ cos θ = \frac{Base}{Hypotenuse} $
$ tan θ = \frac{Perpendicular}{Base} $
$ sec θ = \frac{Hypotenuse}{Base} $
$ cosec θ = \frac{Hypotenuse}{Perpendicular} $
$ cot θ = \frac{Base}{Perpendicular} $
Fundamental Trignometric identities
- $sin^2 A + cos^2 A = 1$
- $1 + tan^2 A = sec^2 A$
- $1 + cot^2 A = cosce^2 A$
Reciprocal Identities
$sin θ = \frac{1}{cosec θ} $
$cos θ = \frac{1}{sec θ} $
$tan θ = \frac{1}{cot θ} $
Trigonometry Table
| Angle | 0°, 0 | 30°, π/6 | 45°, π/4 | 60°, π/3 | 90°, π/2 |
|---|---|---|---|---|---|
| $sin θ$ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| $cos θ$ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| $tan θ$ | 0 | 1/√3 | 1 | √3 | ∞ |
| $cot θ$ | ∞ | √3 | 1 | 1/√3 | 0 |
| $sec θ$ | 1 | 2/√3 | √2 | 2 | ∞ |
| $cosec θ$ | ∞ | 2 | √2 | 2/√3 | 1 |
Periodicity Identities
First Quadrant:
- $sin (π/2 – θ) = cos θ$
- $cos (π/2 – θ) = sin θ$
- $sin (π/2 + θ) = cos θ$
- $cos (π/2 + θ) = – sin θ$
Second Quadrant:
- $sin (3π/2 – θ) = – cos θ$
- $cos (3π/2 – θ) = – sin θ$
- $sin (3π/2 + θ) = – cos θ$
- $cos (3π/2 + θ) = sin θ$
Third Quadrant:
- $sin (π – θ) = sin θ$
- $cos (π – θ) = – cos θ$
- $sin (π + θ) = – sin θ$
- $cos (π + θ) = – cos θ$
Fourth Quadrant:
- $sin (2π – θ) = – sin θ$
- $cos (2π – θ) = cos θ$
- $sin (2π + θ) = sin θ$
- $cos (2π + θ) = cos θ$
Co-function Identities
- sin(90° − x) = cos x
- cos(90° − x) = sin x
- tan(90° − x) = cot x
- cot(90° − x) = tan x
- sec(90° − x) = cosec x
- cosec(90° − x) = sec x
Inverse Formulas
-
$sin^{-1} (-x) = -sin^{-1} x$
-
$cos^{-1} (-x) = π - cos^{-1} x$
-
$tan^{-1} (-x) = -tan^{-1} x$
-
$cosec^{-1} (-x) = -cosec^{-1} x$
-
$sec^{-1} (-x) = π - sec^{-1} x$
-
$cot^{-1} (-x) = π - cot^{-1} x$
Logarithm
Logarithm is the inverse function to exponentiation.
$ \log_a{b} = c \implies a^c = b $
$ \log_2{8} = 3 \implies 2^3 = 8 $
Types of logs
- Common log $\rightarrow$ base 10 $\rightarrow log_10{x} $
- Natural log $\rightarrow$ base e $\rightarrow log_e{x}$ or $ lnx $
- Binary log $\rightarrow$ base 2 $\rightarrow log_2{x} $
Laws of logarithms
Addition Property
$\log_ab + \log_ac = \log_a{bc}$
Subtraction Property
$\log_ab - \log_ac = \log_a{\frac{b}{c}}$
Argument-Power Property
$\log_ab^n = n\log_ab$
Inverse Property
$\log_ab = \frac{1}{\log_ba}$
$\log_a{\frac{1}{b}} = - \log_ab$
Power Property
$\log_{a^n}b^n = \log_ab$
Change-of-Base
$\frac{\log_cb}{\log_ca} = \log_ab$
- $log_a{1} = 0$
- $log_aa = 1$
Problems
Number of digits in an integer
Iterative
count(n){
int cnt = 0;
while(n){
cnt += n%10;
n /= 10;
}
return cnt;
}
Recursive
count(n){
if(!n) return n;
return 1+count(n)l
}
Logarithmic
count(n){
return floor(log(n) + 1);
}
Check if the given integer is a palindrome or not.
bool isPal(int n){
int rev = 0;
int tmp = n;
while(tmp){
int ones = tmp % 10;
rev = rev * 10 + ones;
tmp /= rmp;
}
return rev == n;
}
Factorial of a number
Iterative
int fact(int n);
int res = 1;
for(int i=2; i<=n; i++)
res *= i;
return res;
}
Recursive
int fact(int n){
if(!n) return 1;
return n * fact(n-1);
}
Count trailing zeros in the factorial of a number
int ctz(int n){
int res = 0;
for(int i=5; i<=n; i *= 5)
res += n/i;
return res;
}
TC : O(log5n)
GCD of two numbers
Naive
int gcd(int a, int b){
int res = min(a, b);
while(res){
if(a%res == 0 and b%res == 0)
break;
res--;
}
return res;
}
Time Complexity: O(min(a,b))
Euclidean Algorithm
int gcd(int a, int b){
while(a != b)
if(a>b)
a = a-b;
else
b = b-a;
return a;
}
Optimized Euclidean Algorithm
int gcd(int a, int b){
if(b==0)
return a;
return gcd(b, a%b);
}
Time Complexity: O(log max(a,b))
Extended Euclidean Algorithm
int gcd(int a, int b, int *x, int *y)
{
if (a == 0)
{
*x = 0;
*y = 1;
return b;
}
int res = gcd(b%a, a, &x1, &y1);
*x = y1 - (b/a) * x1;
*y = x1;
return res;
}
LCM of two numbers
Naive
int gcd(int a, int b){
int res = max(a, b);
while(res){
if(res%a == 0 and res%a == 0)
break;
res++;
}
return res;
}
Time Complexity: O(a*b - max(a,b))
Efficient Approach
$\rightarrow a\times b = gcd(a,b) \times lcm(a,b)$
$\rightarrow lcm(a,b) = \frac{a\times b}{gcd(a,b)}$
Time Complexity: O(log max(a,b))
Prime number
Naive approach
bool isPrime(int n)
{
if (n <= 1)
return false;
for (int i = 2; i < n; i++)
if (n % i == 0)
return false;
return true;
}
Time Complexity: O(n)
Efficient approach
bool isPrime(int n)
{
if (n <= 1)
return false;
for (int i = 2; i*i <= n; i++)
if (n % i == 0)
return false;
return true;
}
Time Complexity: O($\sqrt{n}$)
Optimized approach
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
Prime factorization of a number
Naive
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n <= 3)
return true;
if (n % 2 == 0 || n % 3 == 0)
return false;
for (int i = 5; i * i <= n; i = i + 6)
if (n % i == 0 || n % (i + 2) == 0)
return false;
return true;
}
void primeFactors(int n)
{
for (int i = 2; i <= n; i = i + 2)
{
if(isPrime(i))
int x = i;
while (n % x == 0)
{
cout << i << " ";
x = x*i;
}
}
}
Time Complexity: O($nlogn $)
Efficient
void primeFactors(int n)
{
if (n <= 1) return;
for (int i = 2; i*i <= n; i = i + 2)
{
while (n % i == 0)
{
cout << i << " ";
n = n/i;
}
}
if (n > 1)
cout << n << " ";
}
Time Complexity: O($\sqrt{n} logn $)
Using Sieve
void primeFactors(int n)
{
int c=2;
while(n>1)
{
if(n%c==0){
cout<<c<<" ";
n/=c;
}
else c++;
}
}
Time Complexity: O(n)
Print all divisors in ascending order
Naive
void printDivisors(int n)
{
for (int i = 1; i <= n; i++)
if (n % i == 0)
cout <<" " << i;
}
Time Complexity: O(n)
Efficient
void printDivisors(int n)
{
for (int i=1; i*i<=n; i++)
{
if (n%i == 0)
cout << i << " ";
}
for (; i>=1; i--)
{
if (n%i == 0)
cout << n/i << " ";
}
}
Time Complexity: O($\sqrt{n}$)
N Prime Numbers
Naive
void nPrimes(){
for(int i=2; i<=n; i++)
if(isPrime(i))
cout << i << " ";
}
Time Complexity: O($n \times \sqrt{n}$)
Sieve of Eratosthenes
void manipulated_seive(int n)
{
vector<bool> isPrime(n+1, true);
for (int i=2; i*i<=n ; i++)
{
if (isprime[i])
{
cout << i << " "
for(int j=i*i; j<=n; j+= i)
isPrime[j] = false;
}
}
}
Time Complexity: O($ log log n $)
Computating Pow(x,n)
Naive
FOR(1->n) : x = x*x;
Time Complexity: O(n)
Optimized
double myPow(double x, int n) {
if(n==0) return 1.0;
double y = myPow(x, n/2);
if(n % 2 == 0)
return y*y;
else return n < 0 ? (y*y)/x : x*y*y;
}
Time Complexity: O(logn)
Constant Space
$\rightarrow $ Every natural number can be written as the sum of distinct powers of 2.
double myPow(long long int x, long long int n) {
long long int res = 1;
while(n>0){
if(n&1)
res = res * x;
x *= x;
n = n >> 1;
}
return res;
}
Time Complexity: O(logn)
